H法について詳細を記述した文献はありません。以前に学会誌に詳細を投稿したのですが、厳しい査定に心折れて断念しました。タグチの方法以外の計算法については厳しくなってしまうんです。
SCRAP(廃材)になってしまった論文。でも、SCRAP ART(廃材芸術=みんなが不要と思って捨ててしまうモノから、もう一度アートを創り出す)という言葉を思い出しました。諦めたり挫折して一度立ち止まってしまっていたとしても、これで不要とか、それがゴールとかではなく、そこからまた再出発することは可能だし、逆にそれを経験したから得られることもあるのではないか?という言葉を聞きました。それが、この投稿を書こうと思ったきっかけです。
当時は命名されていなかった計算法にH法と名付け、自分で活用していたこの手法。北陸の品質工学研究会で他の会員が使ってみて、その良さを確認していることもあり、北陸研究会以外の人が使うこともあるかもしれない、そのときに詳しい手順を知りたいという要求もあるかと思い、ここに詳細を記述することにしました。参考になれば幸いです。
<研究の対象としていた事例>
超硬合金の素材を製造する会社で、寸法精度を向上する試みがありました。
製品の概要を以下に示します。
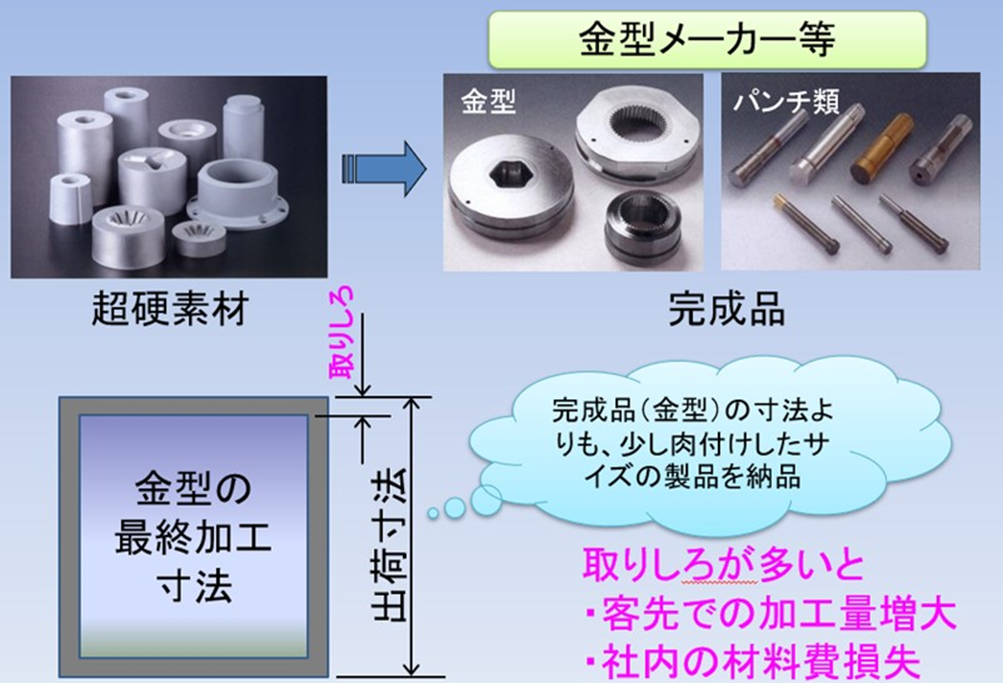
素材の出荷先は金型メーカーです。金型を作るために精密な寸法の金型に加工しますが、目標寸法よりも少し大きい(肉付きのある)材料を購入し、その余分な肉の部分を加工することで、精密な寸法に加工します。余分な肉の部分(図の取りしろ)が多いと、金型メーカーの加工時間が長くなったりツールも摩耗量が多くなったりするので、取り代はできるだけ少なくしたい、そのためには素材の寸法精度を上げることは客先の損失を減らすための重要な品質特性です。
なぜ、寸法はばらつくのか?製造工程概要を以下に示します。
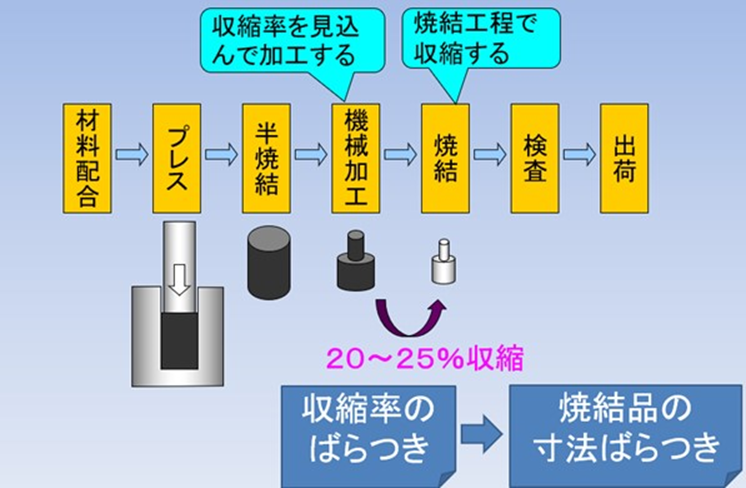
寸法がばらつく最も大きな要因は、焼結時の収縮率がばらつくことです。
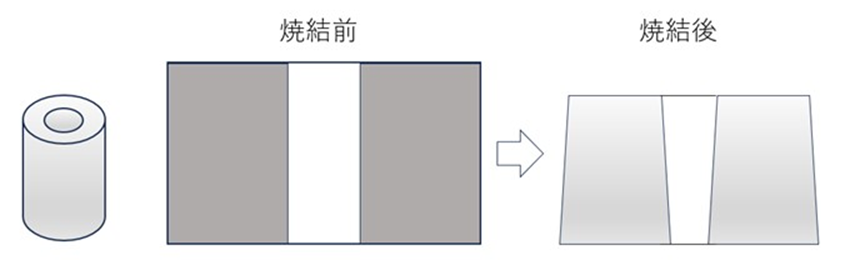
それを改善するために、T法(1)を使って改善してきました。T法の適用は、寸法精度だけでなく、工数削減やリードタイム短縮など多くの効果をもたらしましたが、サイズの大きな製品には適用できませんでした。なぜかというと、サイズが大きくなると収縮+変形が生じるからです。たとえば、下図のような穴のあいた円柱形では、焼結後に変形して上面より下面の寸法が大きくなります。焼結時は液相状態になるため、地球の重力によって下に流れてしまうんです。T法は、収縮は予測できても変形は予測できなかった、ということです。地球に重力がある以上、この変形は避けられません。色々な形状に対して、この変形具合を示す公式というものを定義することは難しいと思います。
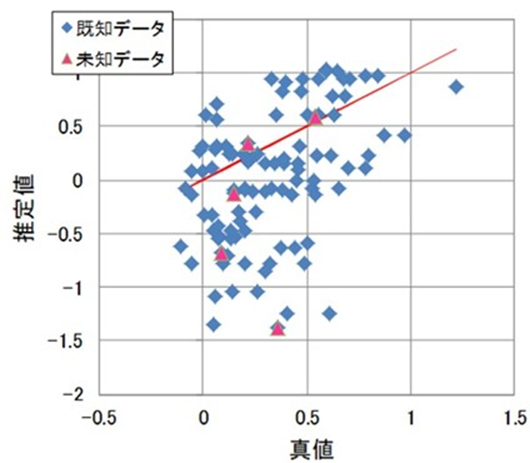
この状況の中で、寸法の大きい(重力による変形が生じる)製品の寸法精度を向上することを検討しました。小さい寸法の製品で成功したT法は、全くダメでした。参考までに、T法で推定したときの真値と推定値との関係グラフを以下に示します。変形を推定できていないことがわかります。
<対策を考えた・H法の原点>
当時は、まだAIがそれほど流行していませんでしたが、後から考えるとAIに近いことをやったんだなと思います。この計算法を研究発表大会で発表したあと、北陸品質工学研究会のイベント発表会でも発表したのですが、AIに近い感じがしたので、比喩しながら説明したものです。
AIの世界では、チェスや囲碁のトップ棋士に勝ち、将棋の世界においてもボナンザが米長邦雄に勝つなど、数年前には想像もできなかったことが起きていました。それに呼応するかのごとく多くの本が出版されました。私が一番参考にしたのは、”人工知能はどのようにして「名人」を超えたのか?”という本です。AIのテクニック的なところから思想まで、とてもわかりやすく読みやすかった本でした。
(注意:以下にはアフィリエイトを含みます)
簡単に概要を説明すると、昔のソフトは、人間の考えていることをコンピューターに教えてきたけど、人間の考えを全て表現することは不可能だった。そこで、まず「教師あり学習」から入り、プロの指した将棋を全てインプットして、その局面でプロはどういう結論を出したかを集計して、類似局面をそこから検索できるようにした。その後「教師なし学習」への進むのですが、そこはちょっと置いておいて、、
人間の熟練者も同じです。過去の経験から類似のものを頭の中から(あるいは過去データの引き出しから)取り出し、それを参考にして対応を決める、という手順です。
そこで、熟練作業者がやっているようなことをコンピューターにやらせよう、っていうのがH法の原点になります。それは「教師あり学習」に似たものといえます。過去データを集めるのは簡単です。それを、どのように結果として導くか?そこにT法の考え方が参考になりました。T法(1)の重み付けという概念が、そのままH法となります。なお、T法に関する参考書籍でオススメなのは、「入門 MTシステム」です。それまで、MTシステムの計算式を具体的に記述した本が無かった、ということもありますが、この本ではT法(1)の式について、変形式も示しており、その式は重み付けしていることをわかりやすく説明できるものなのです。以降、T法やH法の説明をするのに、その変形式を利用させてもらっています。
<H法の計算手順>
考え方の原点
結果を予測するために、過去の類似品の結果を参考にすることはよくあることです。熟練作業者は、この「過去の類似品」に関する情報を頭に詰め込んでおり、その経験を元に判断しています。経験値が多いほど熟練度が高いと評価されるし、実際に色々なケースに対して対応できるスキルとなります。そこで、その情報を電子化してデータベース検索することが考えられますが、リピート品のときは検索値が一致するため探し当てることは容易でも、近似品の検索は難しく、また探すことができても、その集めた情報から解を導く計算も単純ではない。そこで考えた方法は、項目の近さを数値化し、総合的な近さで重み付けする手順です。
なお、前提条件として「過去に似た製品があれば、求めたい値はそのときの製品による実績と近似する」が成立する必要があります。
推定式の概念
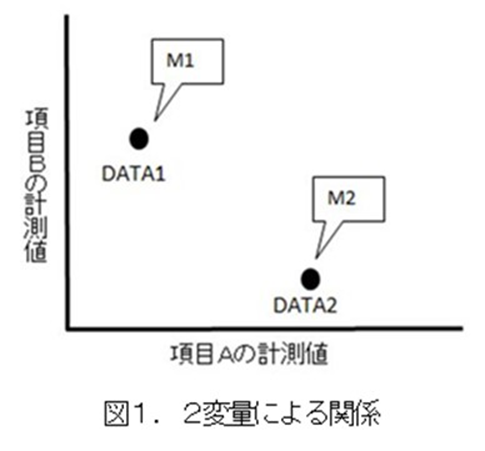
簡単なモデルとして、項目Aと項目Bの2項目とした場合を図1に示します。例えば、項目Aを製品の外径,項目Bを製品の高さとし、求めたい値Mを製品の焼結時の収縮変形率(そのときの実績)とします。縦長(DATA1)の製品と横長(DATA2)の製品では変形の仕方が異なります。図の座標が同じであればそれはリピート製品であり、当時生産した製品の収縮変形率を参考に現在の製品を製造します。座標が一致しなくても、近い位置にあれば、類似な製品と考えるのは自然なことです。
実際の項目は数多く存在するため、これを多次元ととらえた近さを評価します。
まず既知の情報を集め、それをDB(データベース)空間とします。T法でいう単位空間の位置づけですが、この場合は標準的な値ではなく、単に既知の情報でしかないのでDB空間と呼ぶことにしました。図2の黒い点をDB空間の座標とします。図2はイメージし易いように2項目の場合の座標で示しますが、実際には多次元の座標です。ここに、推定したい条件の座標(図の■)を入れた時、その近さで重みづけします。たとえば近い3点で推定する場合、近さの比率を仮に50%,35%,15%としたとき、最も近い点の真値×50%+2番目に近い点の真値×35%+3番目に近い点の真値×15%で推定値を計算するイメージです。
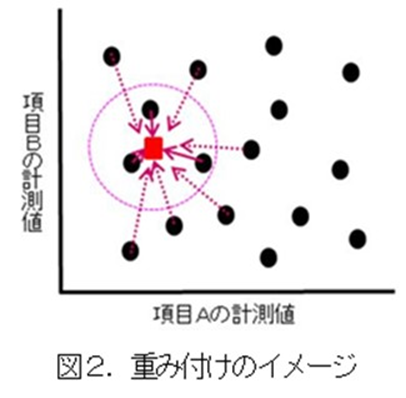
なお、ここでいう真値は、絶対に正しい値ではありません。あくまで過去の実績であり、ばらつきが含まれます。同じ条件で製作しても、前回と今回で全く同じ値にはならない可能性があります。よって、できるだけ多くの類似品で推定したいはずです。
計算手順
1)DB空間となるべきデータを集める(n個)
データ数は多いほど良いでしょう。できるだけ多くの形状が含まれているほど良いし、同じ形状でも数が多いほど良いです。集めたデータを表1に示します。表1の”項目”とは、予測のための情報でk個,真値(M)は求めたい特性値でn個とします。
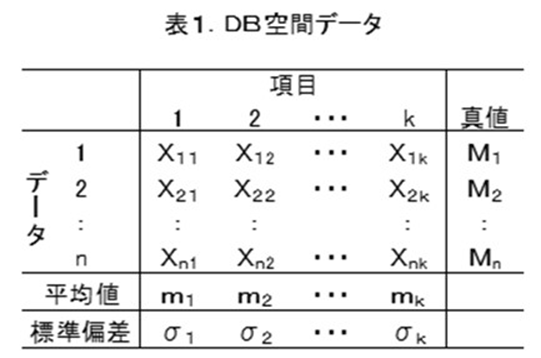
2)DB空間のデータを規準化する。
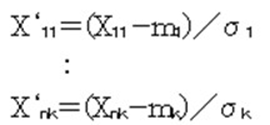
規準化したデータを表2に示します。
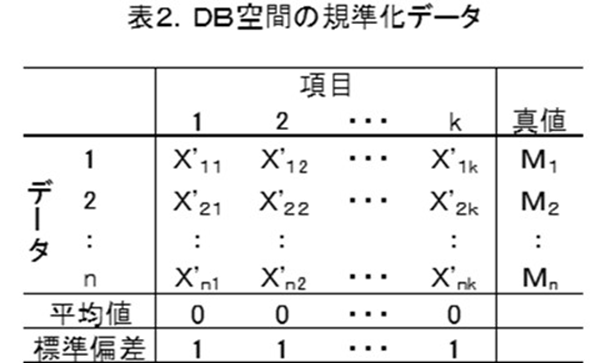
3)多次元の座標差を求める
変形率を求めたい製品の項目値を規準化し、DB空間の規準化した値それぞれから差し引きます。
求めたい製品の規準化した項目値を
y‘11,y’12・・・y‘1k とすれば、
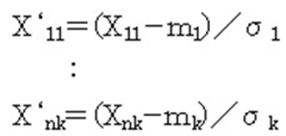

4)差分の分散を求める
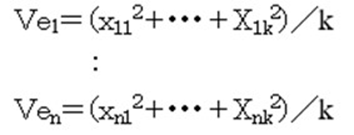
5)ηを求める
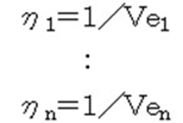
表4にηと真値Mを代入して表5に示します。
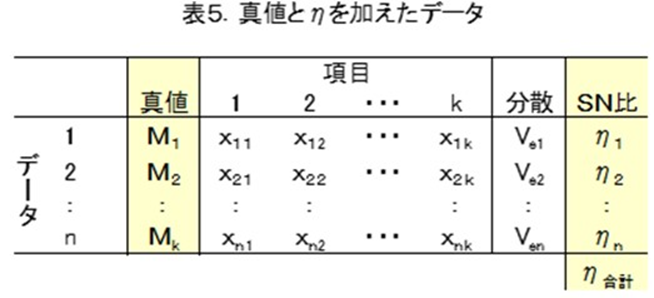
この時、推定したいデータと全く同じ情報(リピート製品)がDB空間にあったときには、Veが0になりηを計算できません。その場合、計算できない行以外のηの最大値の数倍を代入するといった近似が必要となります。(詳細は後述)
6) 閾値よりも大きい値を除外する
Veまたはηについて閾値を決め、
a)それを超える値については以降の式に使わない。
b)最も小さいVe(または最も大きいη)が閾値を超える場合には推定値を計算しない。
という処置が必要になります。閾値を超えても物理的に計算は可能ですが、閾値外のデータの数が多いほどそれらに引っ張られるため推定精度が落ちるのです。
7)推定値を求める
推定値は、各行の真値をηで重み付けして合計します。推定値M=(η1・M1+・・・+ηn・Mn)/Ση
なお、この式の中に、閾値から外れた行は含まれていません。またΣηにおいても閾値以内の行だけの合計です。
計算手順に関する補足
ここまで述べた計算手順を決めるに至った理由について、実験データを交えて補足します。
1)Veが0になり計算できないとき
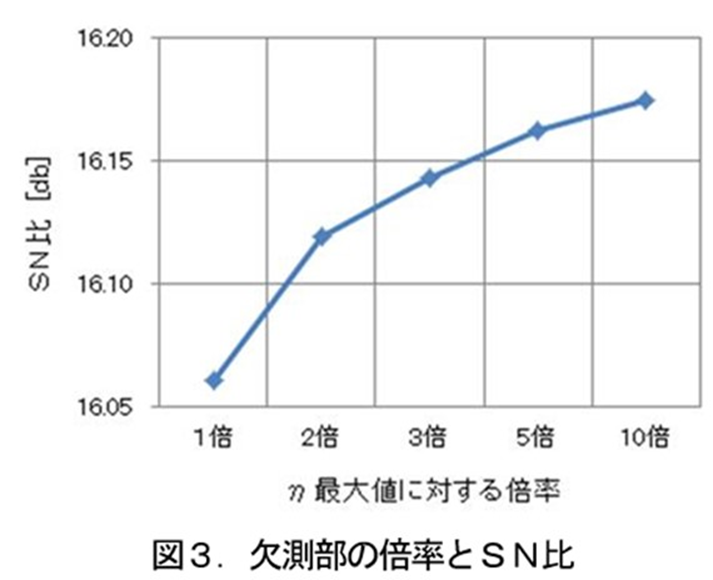
Veが0(ゼロ)になると、物理的にηが計算できません(0で割れないので)。Veがゼロということは、リピート品だということであり、過去データの真値をそのまま解として適用することも考えられます。過去の実績にばらつきがほとんど無いものであればそれでも良いかもしれません。しかし、過去データはそのときに得られた結果であり、同じように製造してピッタリ再現するか疑問であるなら、できるだけ多くのデータで推定したほうが信頼できます。そこで、計算できない行(Ve=0の行)以外でηの最大値の数倍を代入することを考えました。実際に何倍が良いのか、事例を元にシミュレーションしてみた結果を図3に示します。横軸は欠測部に代入する値を計算するときのη最大値に対する倍率です。縦軸のSN比は、推定した値と実際の値との関係です。(真値Mに対する推定値をyとしてy=βMで計算したSN比=ばらつき)この結果を見れば、倍率は大きければ大きいほど良いことになるのですが、あまり倍率を高くしすぎるとリピート品の値に結果を引っ張られる恐れがあるので、ある程度飽和する3~5倍程度が良いのではないかと考えましたが、適用事例(db空間のデータ数など)が変われば別の傾向になる可能性もあるので、単純に「何倍がいい」といった定義は難しいです。
2)閾値を設ける理由
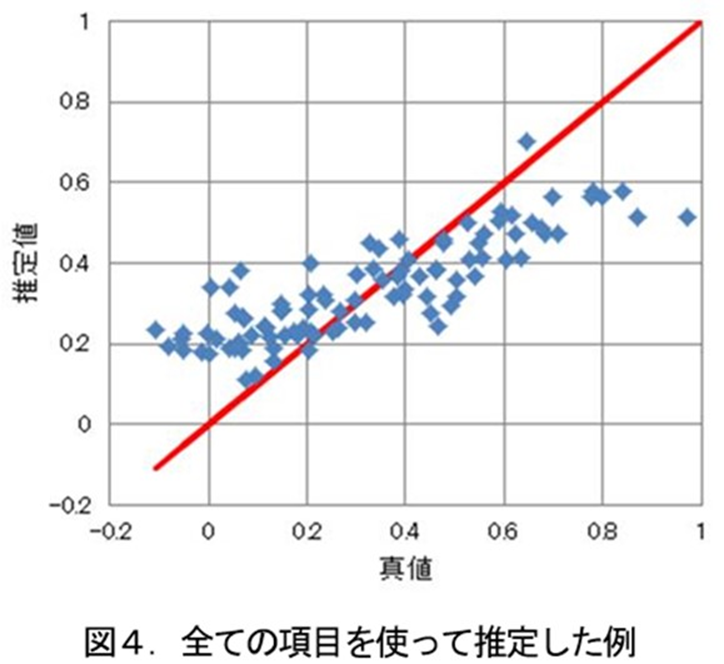
Veまたはηについて閾値を決めなくても、理論的には正しいように思えます。T法(1)も気にせず全ての項目を使うのが良いとしています。最初は、距離が遠い条件は寄与率も低いのだから影響しないと考え、全ての項目を使って計算しました。その結果を図4に示しますが、推定値が中央の値に近づいていく傾向が確認されました。つまり、距離が遠いデータは、寄与率が低くても、数が多いと推定結果に影響を与えてしまうとわかったので、寄与率が少ないデータはできるだけ省いたほうが良いと判断しました。そのため、閾値を決めて選別します。
3)閾値の決め方
では、どのような基準で閾値を決めるか?残念ながら明確な答えはありません。閾値を厳しくするほど推定精度は良くなるけど、同時にその範囲に入る対象は少なくなります。厳しすぎれば閾値に入る過去データが無くなります。(近い条件の過去製品が無いということは、そういう結論でムリに答えを求めないことも正解ですが、データが多く集まらないと計算できないというのも実用上困ります)逆に閾値が甘ければ、推定精度は悪くなります。超硬合金の事例においては、何度かシミュレーションした経験をもとに最低限の精度を守れる閾値を設定しました。最初、データが少ないため閾値内に入る過去データが無いことがありましたが、その場合はこの計算式を適用せず旧来の手順で計算しました。そして結果を順次登録できるプログラムにしました。(学習機能)DB空間を蓄積していくことで計算不能件数は徐々に減り、閾値もまた徐々に厳しい方向へ修正することが可能になります。
4)項目の層別
項目の層別も重要です。超硬合金の事例でも、最初は単純に計算してみましたが精度に不満があり、対策をいろいろ検討した結果、層別することで推定精度を改善することができました。
超硬合金の事例への適用
冒頭に述べた超硬合金の寸法精度改善(収縮+変形率の推定)に適用した結果が図5です。横軸が真値で縦軸が推定値。期待する推定精度が得られました。
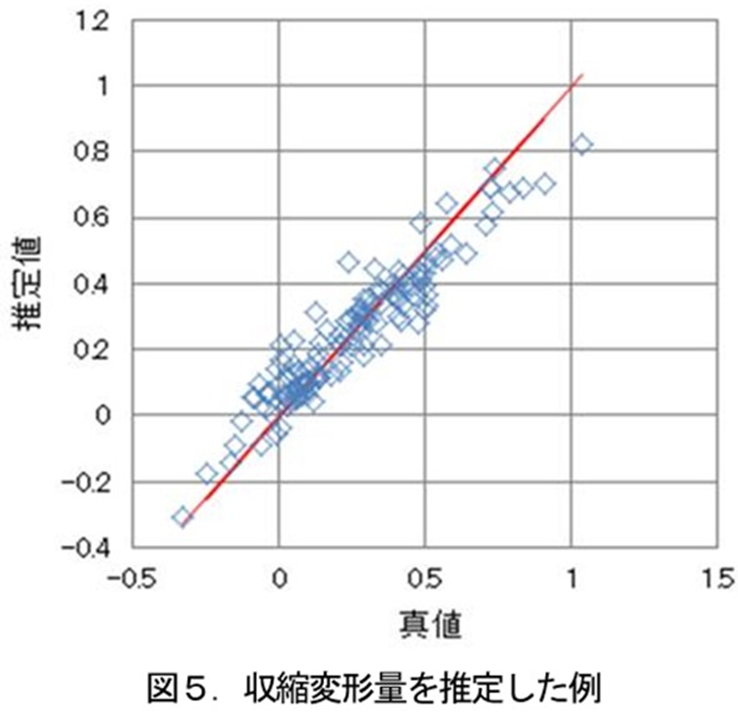
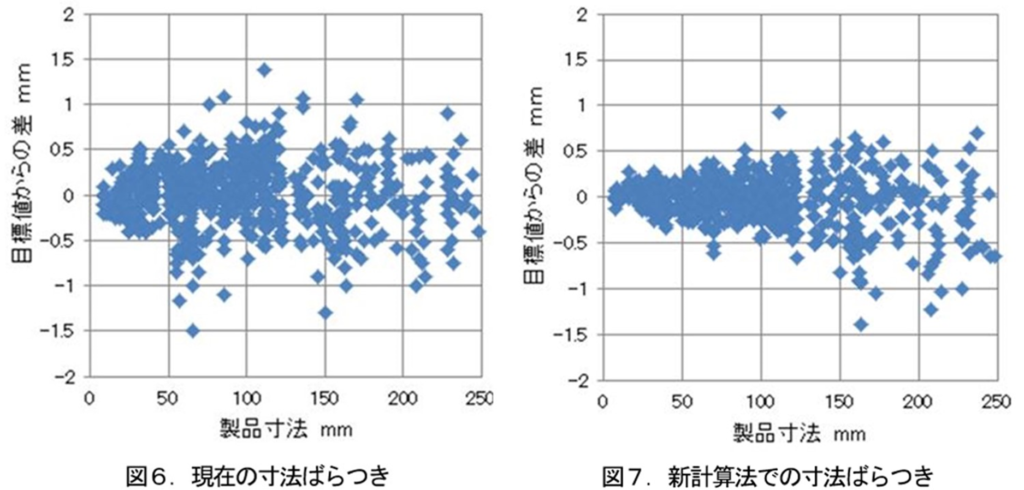
改善効果についてグラフで表示します。図6は従来条件、つまり実際に現場で運用している計算基準で推測し加工した製品における、目標値からの差のばらつきを図示したものです。差は製品寸法が大きいほど大きくなるので、横軸は製品寸法にしました。この個々のデータに対して、今回の計算式を用いて推定した場合のデータが図7です。(注:計算上の推定値です)SN比で2.85dbの改善効果でした。この時点ではまだDB空間のデータは少なく、今後実績を積み上げてDB空間を増やすことでさらに精度向上することが期待できます。データ数が少ない「寸法の大きい製品」のばらつきが大きいことがグラフからも顕著に読み取れると思います。
まとめ
熟練者が頭の中で行っている判断を自動化して、初心者でも同じ計算ができるようにするための推定式としてH法を考案し、ここではその詳細について解説しました。まだ適用事例が少ないのですが、実践を積み重ねることで成果や課題がもっと見えてくると期待しています。
Q&A
Q1 従来条件に対して新計算法の推定ばらつきは減少しているが、成形品の場合では成形条件を変えない限り成形品そのもののばらつきは変化するわけではない。製品のばらつきでなく評価のばらつきが改善したのか。
A1 評価 (推定精度)のばらつきが改善することで、結果として製品のばらつきが改善した。成形品は金型形状(目標値)が固定で、大量生産における製造ばらつきを評価しているが、今回の事例の場合は推定した収縮変形率をもとに成形加工のネライ値を変えている。プロットしているデータは、全て形状が異なった製品のものである。
品質工学の本質から考えれば、まずは製造ばらつきを改善して、次に目標値にチューニングするのが良い。今回の事例は、製造工程のばらつきを改善していない。本質を追究するなら、製造時のばらつきを改善すべきだし、変形の起こらない条件(重力の無い環境での焼結,あるいは液相でなく固相焼結による製造など)の検討をすべきかもしれないが、難易度が高い。
最終製品のばらつきには、製造のばらつき+推定のばらつき(加工の目標値を決めるときのばらつき)が含まれるので、今回は推定のばらつきを改善した事例である。
参考文献

