品質工学のMTシステムはいろいろなところに使える解析方法で、会社でも多く使われていますが、農業の分野でも使われています。たとえば、2022年度の品質工学研究発表大会では「ニオイセンサを用いたMT法によるマスクメロンの熟成モニタリング」という事例が発表されています。
ここでは、私の家で生産している干し柿の乾燥条件について、MTシステムの各手法を使って解析比較した事例を紹介します。MTシステムは、MT法(マハラノビスタグチ法)が始まりで、その後改良されたT法などをまとめて「MTシステム」と呼んでいます。
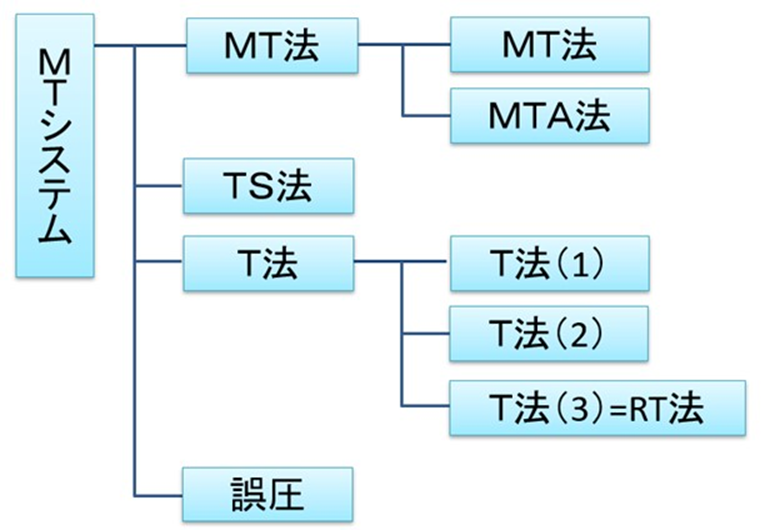
干し柿の事例を通して、各手法の特徴や精度を比較してみたので、以下に紹介します。
そもそもの始まりは、私事ではありますが、家が干し柿を生産する農家で、おせじにも上手いとはいえないレベルの品物を出荷していました。ある年、父親の逝去により母親が中心に面倒をみることになり、近所の上手く作る家の人にいろいろ聞きながらやってみたところ、例年にない(家にしてみれば)きれいな干し柿を作ることができたのです。さて、今回はうまくできたけど来年もできるか?手元にあるのは段ボール紙に書かれた乾燥記録のみ。今年のと前年(下手だったとき)のデータがある。では、MTシステムで解析することで上手に生産する条件を標準化することができないか?というのがこの解析を行うキッカケでした。
まずは干し柿の生産工程を説明します。
10月中旬ごろから収穫できます。
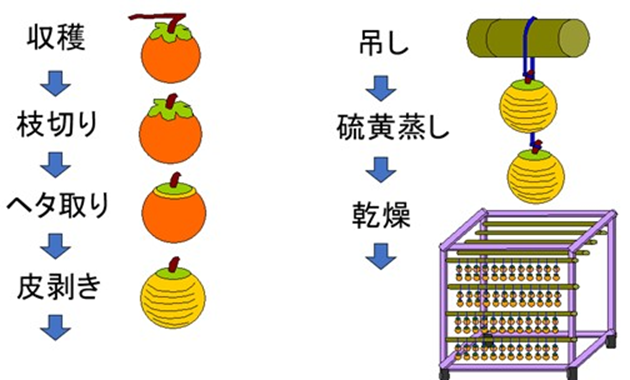
川を剥いた柿は2個ペアで紐で縛り、竹竿に吊します。それを台車に数十本付けます。
乾燥は台車単位で、大きな乾燥機に出し入れして行います。
下図の表は、乾燥間隔を見やすくするために表したもので、横軸は時間(日にちと、細かい縦線は2時間単位です)、縦軸は台車No.です。青い部分が乾燥機に入れている時間です。最初の台車は11/4に12時間乾燥機に入れ、数日自然乾燥,11/8に2回目の乾燥を12時間・・・というふうに読みます。
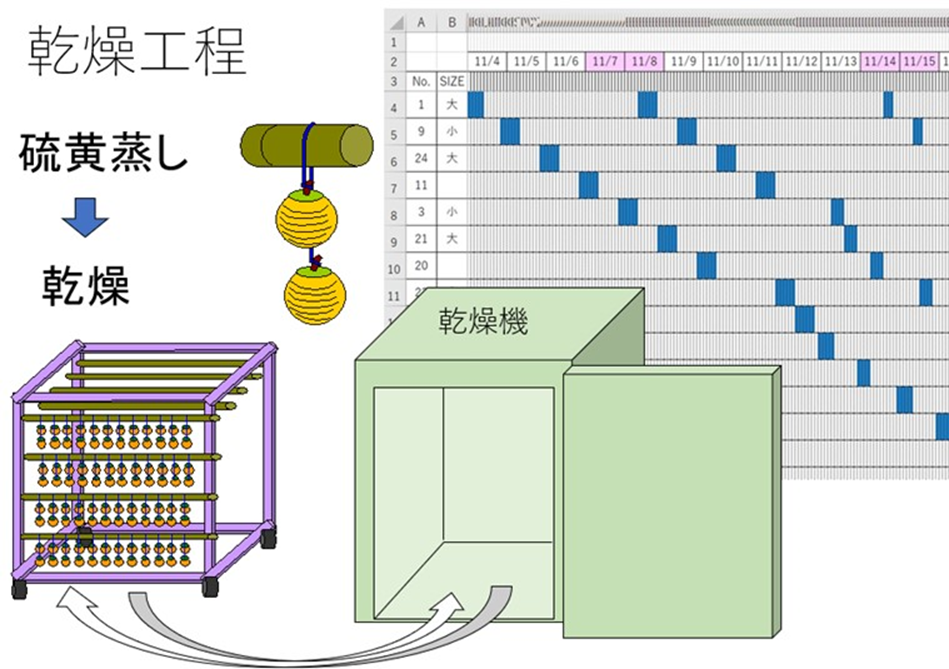
台車に付けられた段ボール紙に、乾燥機に出し入れした記録をマジックで書いているので、それをEXCELに入力ました。

この乾燥の仕方によって、干し柿の外観は大きく変わります。どれくらい違ったかというと、下図に示すように、下手なときは黒かったり黄色かったり、シワが多かったり。乾燥条件が変わることで比較的きれいなものができました。その中でも数個、特にきれいだと思えるものが、「理想」とするところです。しかし4台車ほどは、少し粉が吹きすぎたイマイチな状態に仕上がりました。白い粉が多いので「雪降り」と名付けました。

さて、段ボール紙に書かれた情報をそのままEXCELに代入すると以下の表のようになりますが、このままでは解析できません。
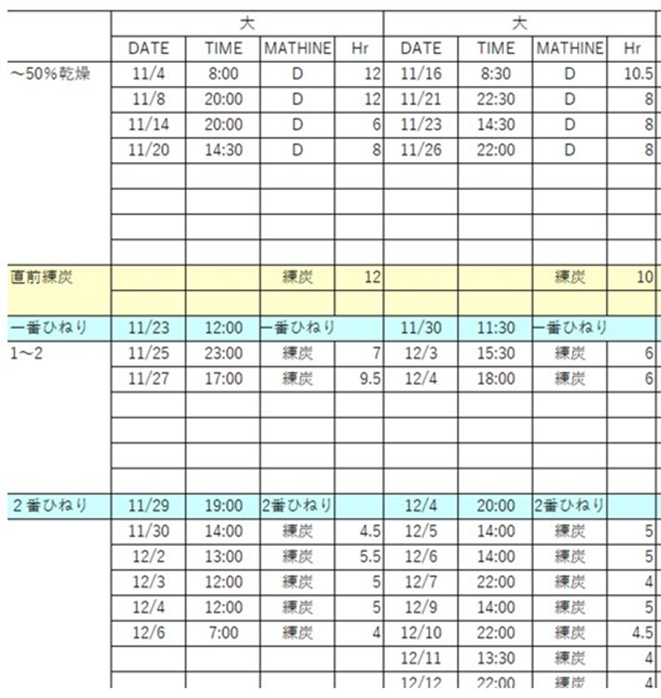
そこで、ザックリ項目を決めて変換しました。
項目は15項目、正常な台車が9台,雪降り(粉が多くて少し不満)の台車が4台,変色(乾燥が下手で色がわるいもの)が6台です。※通常は項目が横軸なので、解析するときは縦軸横軸を逆に修正しています。
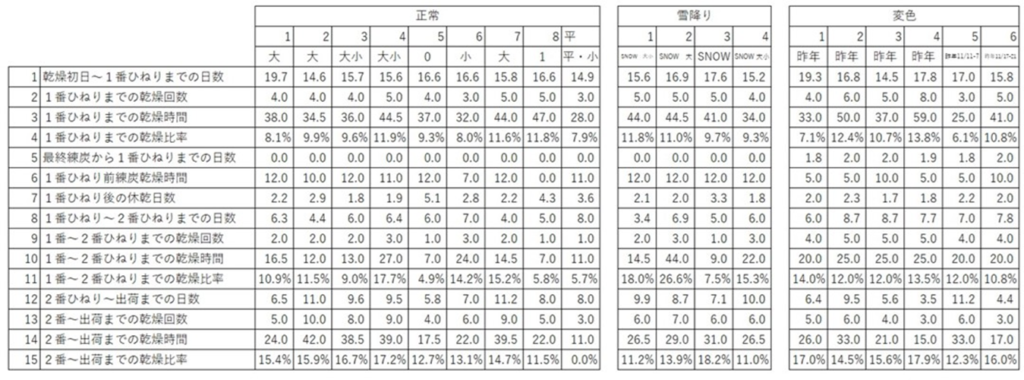
生データをグラフにしてみました。
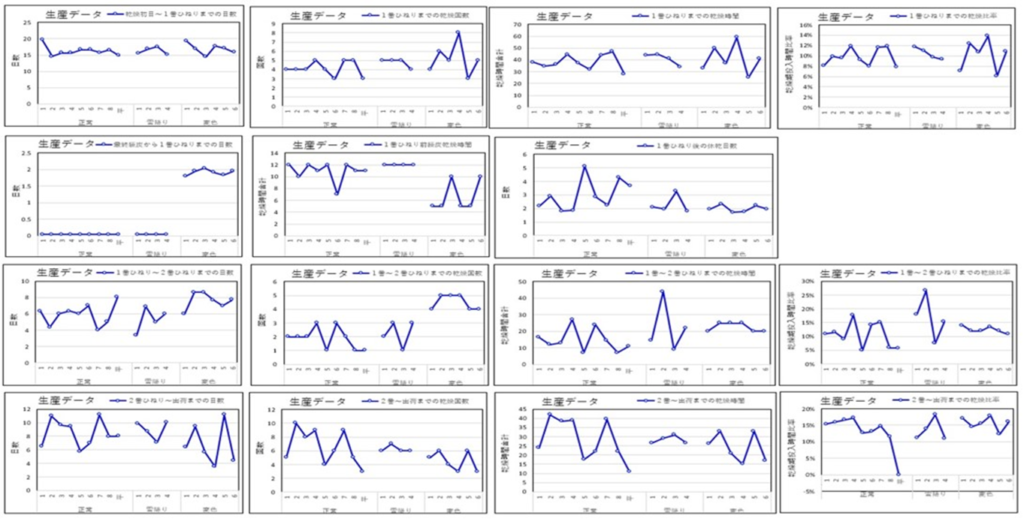
各項目毎に比較しても、正常・雪降り・変色を区分けできませんよね。そこでMTの登場です!
え?ちょっと待て、5番目の項目は変色だけ大きく差があるんじゃね?
と思われた方がいると思います。はい。その通りです。実は、変色になる要因、つまり昨年と今年で大きく差が出た原因は、5項目の条件だったのです。そこは明確に確認できました。MT解析するまでもなく。
そこで、目的がちょっと変わってきました。MT法で解析して、変色が異常と判断されるのは当然として、その解析方法で正常と雪降りを区分けできるか?という、少しハードルが上げられた判別に挑戦することになりました。各計算方法の優劣がうまく比較される条件になってきました。楽しみですね(^^)
MT法による解析
MT法は正常なもののデータを集めて基準空間とし、基準空間からの差の大きさで正常か異常かを判別する方法です。マハラノビスの距離という値を計算します。
正常な9台車のデータを規準化~相関行列の作成~逆行列に変換~マハラノビスの距離を算出。
正常なデータは1を中心にばらつきます。
基準空間の逆行列データを使って、雪降り、変色のデータも同様にマハラノビスの距離を求めます。
その値が1から遠いほど、基準空間との差が大きいと判別できるのです。
計算してみると・・・
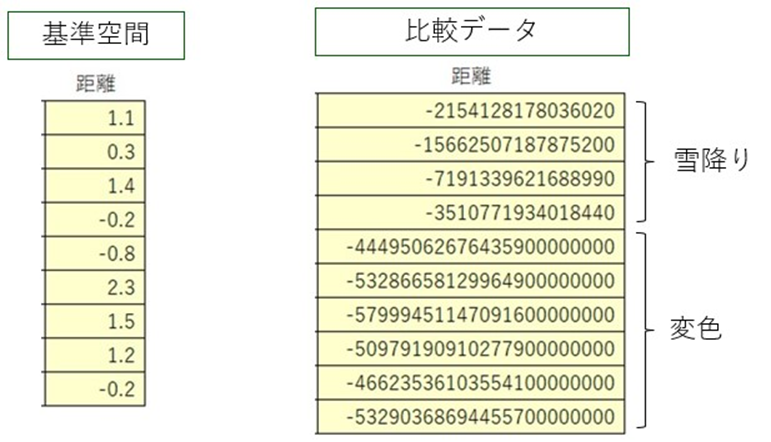
雪降りと変色の距離は、異常に大きい!桁を数え切れないくらいに。。
これはAIでいうところの過学習という状態ですね。
基準空間のデータが少ないと、MT法はうまくいかないんです。
項目数15に対してデータ数が9個でした。通常は項目数の3倍ほど必要と言われています。
MT法は基準空間のデータが少なくてダメでした。で終わっても良いのですが、「データ数が多ければどうなるの?」という質問もあるかと思い、変則的ですが、基準空間のデータを嵩増しして計算してみます。
直交表L12を使って、基準空間のデータを膨らませてみました。基準空間のひとつのデータに対し、L12の水準に合わせて±xσを加減したデータを追加しました。xの値はいくつが妥当かはわからないので、何通りかで距離を計算して比較してみました。
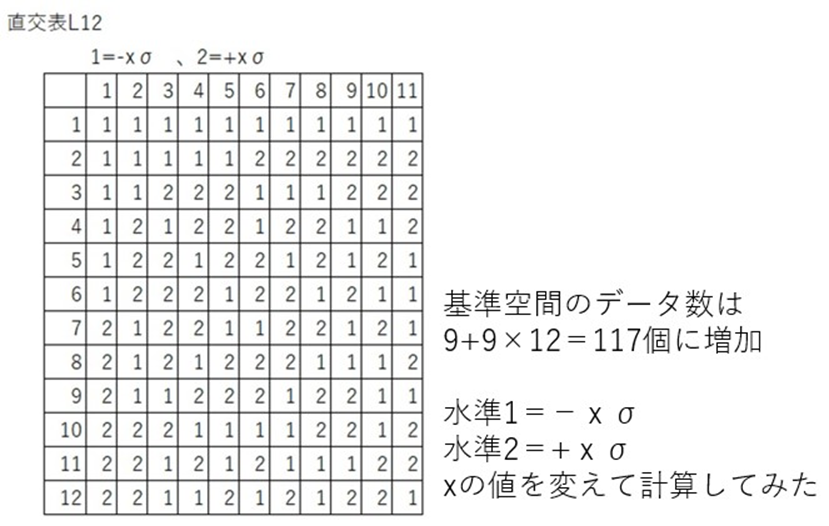
σの倍数xを1,0.5,0.25,0.1 の4通りで、距離の値をヒストグラムに現してみました。
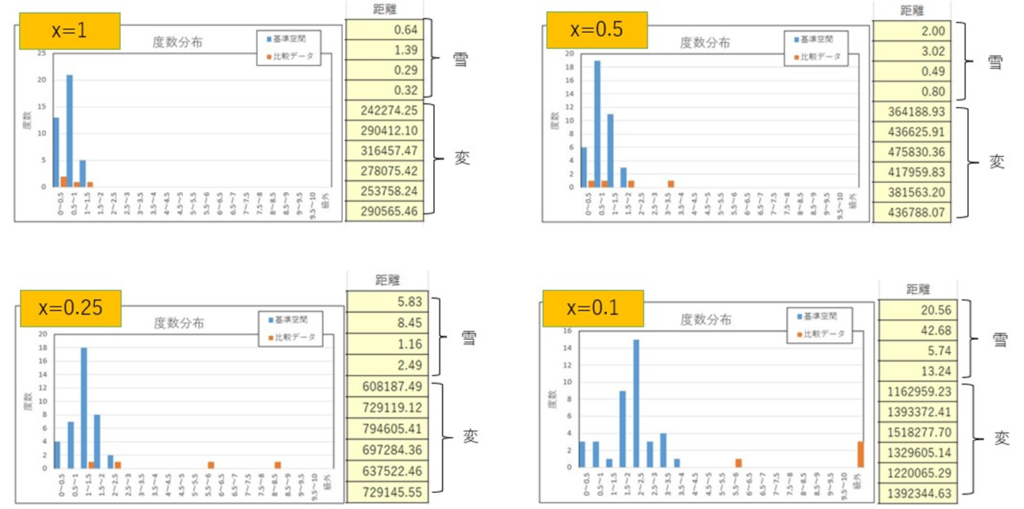
全ての条件で、変色は圏外の異常に大きい値にまりました。雪降りについては、xの値が小さいほど距離が大きくなっているのがわかります。xを適度な値(0.2ほど?)にすると良さそうではありますが、過学習な状態は改善できていない感じはします。ただ、基準空間を増やすことで、まともな解析結果に近づいたとはいえそうです。
MT法はこのように基準空間の数が少ないと計算できない(過学習になる)という欠点があります。
それ以外にも、類似のデータがあると多重共線性により計算できない、逆行列が計算できない、などといった問題もあります。それを改善する計算の工夫でMTA法などもありますが、処理時間がかかるということも含めて少し扱いづらい計算法かもしれません。
RT法による解析
RT法は、MT法の欠点を改善して簡素な計算式にしたものです。精度はMT法よりも劣りますが、基準空間のデータが少なくても良い、多重共線性があっても計算できる、計算式が簡素なので処理速度が速い、EXCELでも計算しやすいなどのメリットがあります。具体的な計算手順は省略して結果のみ表示します。
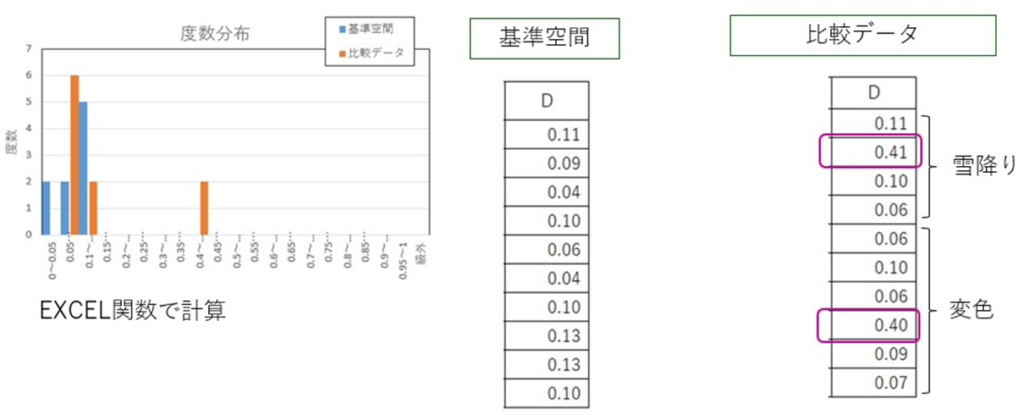
RT法では、変色も雪降りも明確な(基準空間との)差がなくなってしまいました。変色すらも検出できないとはお粗末です。なぜそのようなことになったのでしょう?RT法の計算式がそういう性質があるということですね。
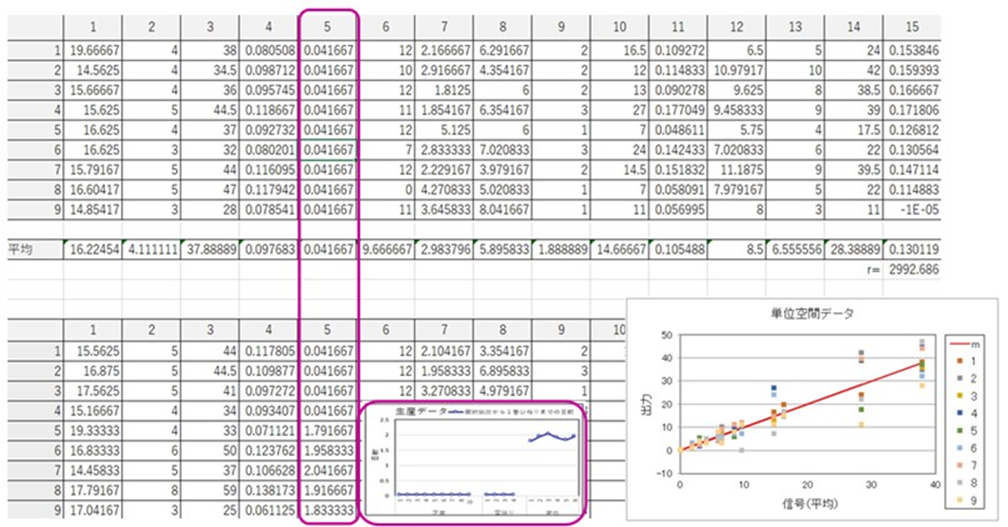
RT法は単位空間(MT法でいう基準空間)のデータについて、その平均値を信号(M)としたy=βMの関係を求め、SN比(ばらつきの逆数)と感度(平均的大きさ)の値で行列式を作ります。
変色に影響の大きい項目5の値は0.04~2くらいですが、信号MはMAX40まであります。小さい値が多少変動するより、大きい値が変動した影響のほうが大きいのです。
RT法は、項目の値が極端に違う場合にはこのような問題があるので、一般的には項目の単位が同じ場合に使われることが多いのです。(画像の評価などは得意でしょう)
この問題(データ単位)に対する解決策について、
品質工学会の学会誌「品質工学」Vol.31 No.3 pp11-16に解説が掲載されました。
解決策は、以下の2つの方法のどちらかを使うと良いとのことです。
(1)正規化する・・・平均値を引いて標準偏差で割る
(2)平均値で割る
解決案の提案通りに、再度計算してみました。
(1)正規化
単位空間データ(正常なサンプル)について計算しましたが、項目5については全てが同じ値のため標準偏差の計算値がエラーとなり計算できませんでした。
(2)平均値で割る
結論からいうと、この平均値で割るという手段は、今回のデータについては有効でした。
結果のグラフを以下に示します。変色は明確に差がでています。雪降りについては4台車中1台車は区分けできましたが、3台車は正常品との差をつけられませんでした。
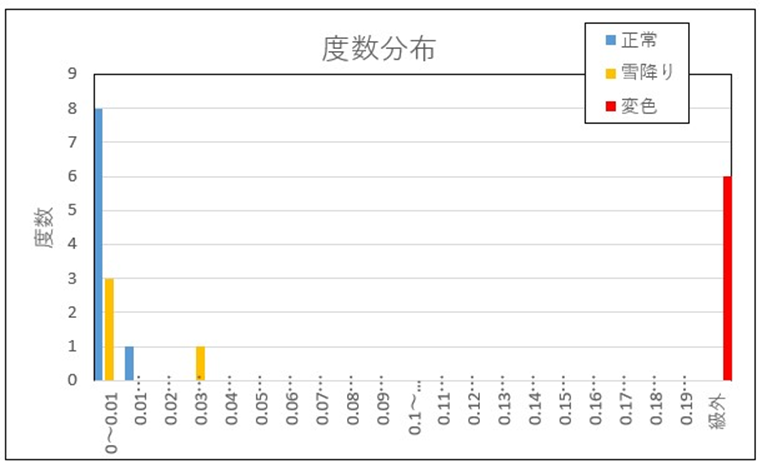
RT法は、データ単位が共通でないと使いにくい計算方法ですが、上記のような対策(今回は平均値で割る)を行うことで対応できることを確認しました。MT法よりも計算が簡単(EXCELの関数で自動計算できるレベル)で、そこそこの判別はできるので、扱いやすい計算方法だといえます。
標準化誤圧による解析
標準化誤圧は、品質工学創始者の田口玄一先生が亡くなられてから見直された解析方法です。
2000年に「標準化と品質管理」誌に掲載されたのみで、それ以降議論されることがなかったのですが、後継の人たちによって再検討され、2010年に矢野氏らによる研究論文が学会誌に掲載されました。それ以降、RT法よりも誤圧のほうが使われる頻度が高くなったように思います。
今回のデータを、誤圧で計算した結果、
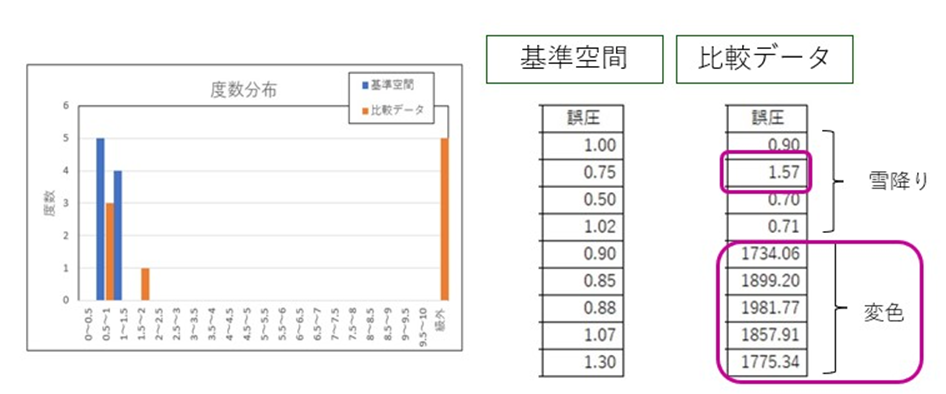
変色は明確に差がでたのですが、雪降りは4台車のうち1台車のみ少し大きくなった程度でした。
※この結果はRT法と同等レベルです。
標準化誤圧の評価は、じつは単純に誤圧を計算するものではないと思います。2000年に掲載された論文も、全体誤圧から徐々に分割を広げた誤圧を計算することで精度を上げています。今回の事例も、段階毎に分類して誤圧を計算することが必要と思い、工程を3分割して計算してみました。
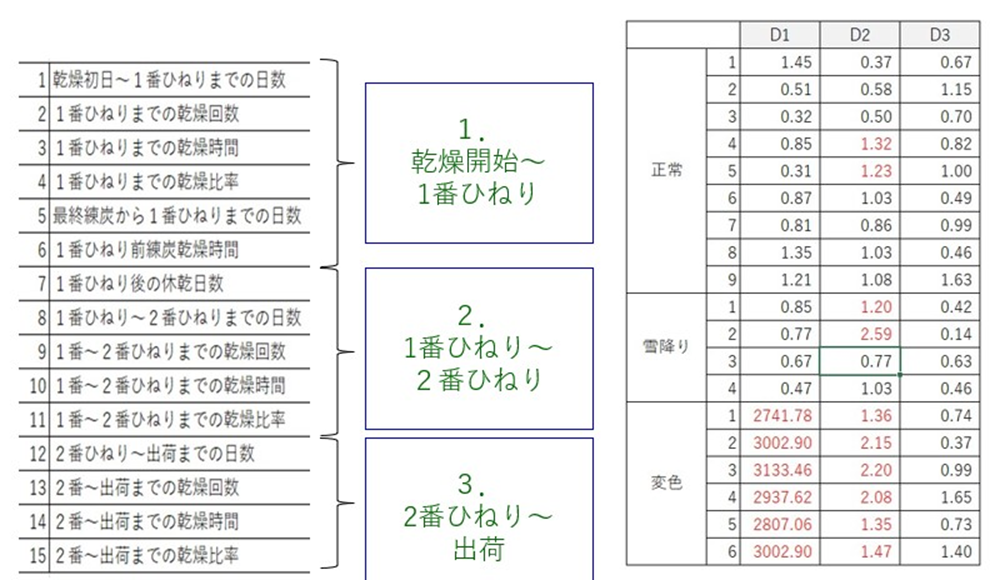
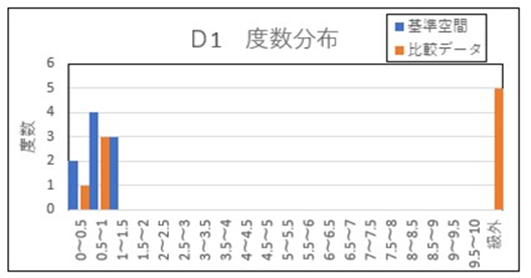
最初のブロックD1(項目1~6)で変色を判別しています。変色には項目5が大きな要因になっていることがわかっているので、期待通りの結果です。
第2ブロックD2(項目7~11)でも変色が大きくなる要因がありそうです。しかし雪降りを完全に区分けすることは難しいようです。第3ブロックD3(項目12~15)には差が見られませんでした。
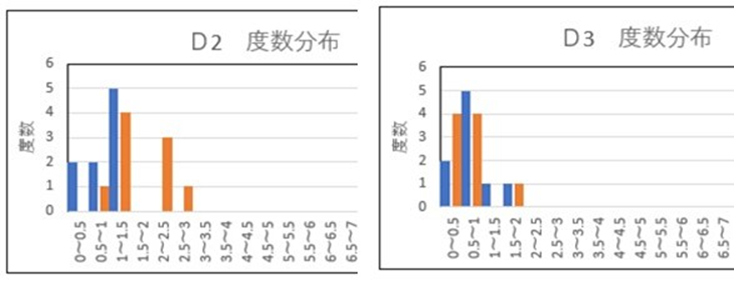
誤圧の評価では、項目1~12の工程で外観に差が生じると推測できそうですが、雪降りがどの工程条件(項目)に起因するかまでは分類できませんでした。
T法(2)による解析
T法でも解析してみました。T法は、正常か異常かを判別するものでなく、具体的な値を推定する計算法なので、ここでは外観にザックリ点数をつけて計算してみました。
正常:0点
雪降:2点
変色:10点
具体的な値があるときはT法(1)ですが、基準点がゼロの場合はT法(2)になります。計算手順は同じです。
T法で推定した値をグラフにしてみました。横軸が真値で縦軸が推定値です。赤い線が真値のラインです。真値10点のところに推定値は9~11くらいの値でばらついており、変色(10点)の推定はうまくいっています。雪降り(2点)については0点付近にばらついており、正常と差が無い状態です。
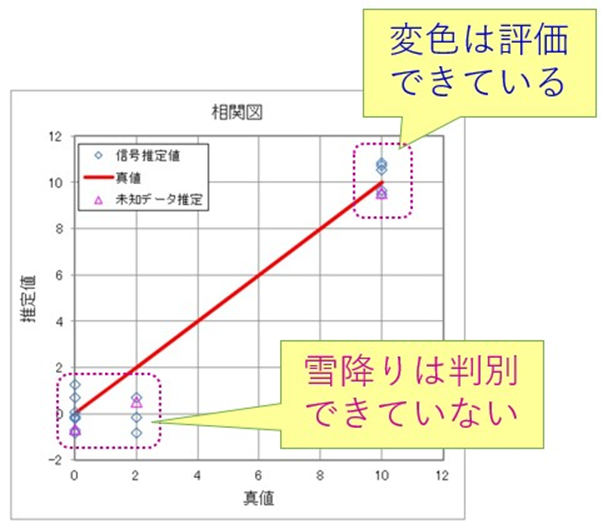
参考までに、項目選択を計算し、どの項目が影響しているかをみてみました。
項目選択とは、2水準系の直交表を使って、その項目を使うか使わないかを、水準1「使う」水準2「使わない」として計算し、真値と推定値との差(SN比)を評価するものです。SN比が高い=真値と推定値との差のばらつきが小さい、ということなのでSN比は高いほうが良いということです。水準1のSN比が高ければ、その項目は使ったほうが良い、逆に水準2のほうが高ければ、その項目は使わないほうが良い、と考えられます。
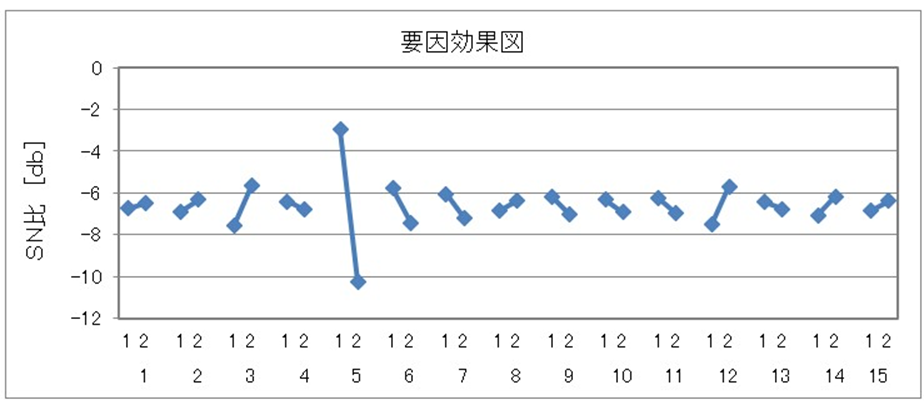
項目5だけ大きく水準差がでました。(水準1が高いので使うべきという判定)
変色に対して項目5が大きくきいている、という結果がでました。
(変色が項目5に起因しているという程度は判断できる)
しかし、雪降りは全く差が出ていないので、RT法や誤圧よりも判別精度は落ちそうです。
※もともと値を推定する計算法なので、使い方は間違っていますが。
H法による解析
H法は、過去データを参考にして、過去のデータベースに近い条件から重み付けして値を推定する解析方法です。詳しくは品質工学研究発表大会RQES2013予稿集「T法の推定精度向上の検討」を参照してください。
H法も具体的値を求める計算方法なので、T法と同じように点数をつけて解析しました。点数は以下のようにザックリきめました。
正常:1点
雪降:3点
変色:10点
全データから、3個(正常から1個、雪降りから1個、変色から1個)抜き取ったデータをDB空間データとし、その値を使って未知データ(抜き取った3個)を推定できれば成功です。
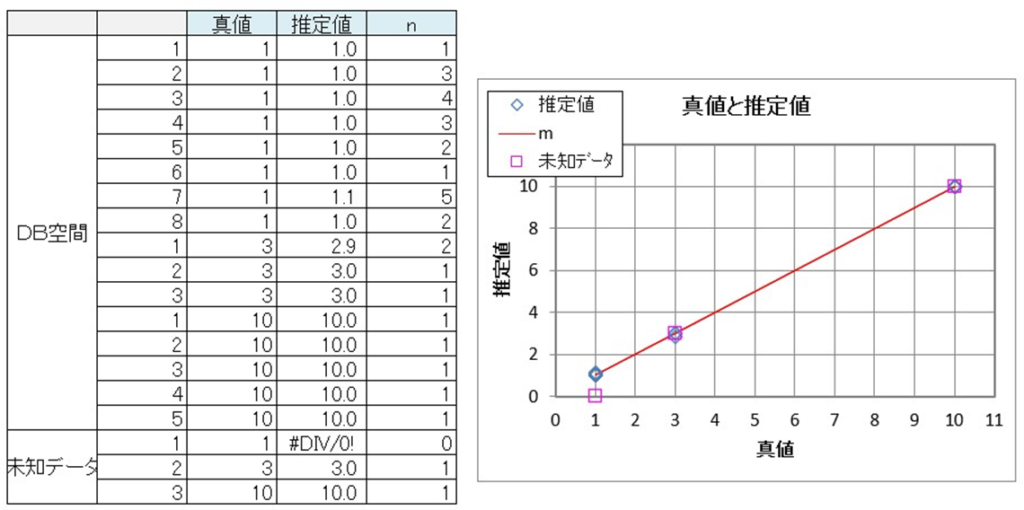
真値-推定値のグラフを見ると、未知データの雪降りと変色はきれいに線上に乗りました。
未知データの正常品は、計算エラーになってしまいました。これはどれくらい近いかという閾値に入るデータが無かったためです。そこで、閾値を徐々に大きくして近似データが現れた段階で推定計算すると、推定値は1(真値と同じ値)になりました。ただし閾値を広げるのは問題があるので、参考です。
DB空間データの推定値は、その値を含むので、線上に乗って当然です。あくまで、DB空間にない未知データを推定できるかということがポイントになりますが、かなり良い結果になりました。
しかし、n数(推定につかったDB空間の既知データ数)が1になることが多く、とくに雪降りと変色は1個が多いし、未知データも1個だけの既知データを使った推定値になってしまうので、過学習になっている感じは否めません。H法はDB空間のデータが多いほど(AI的にいうと学習するほど)精度が高くなりますが、今回のデータはDB空間の数が少なすぎて不安があります。しかし、これまでの各計算手法のなかで一番可能性を感じたのはH法でした。
項目選択を行ってみました。手順はT法と同じです。
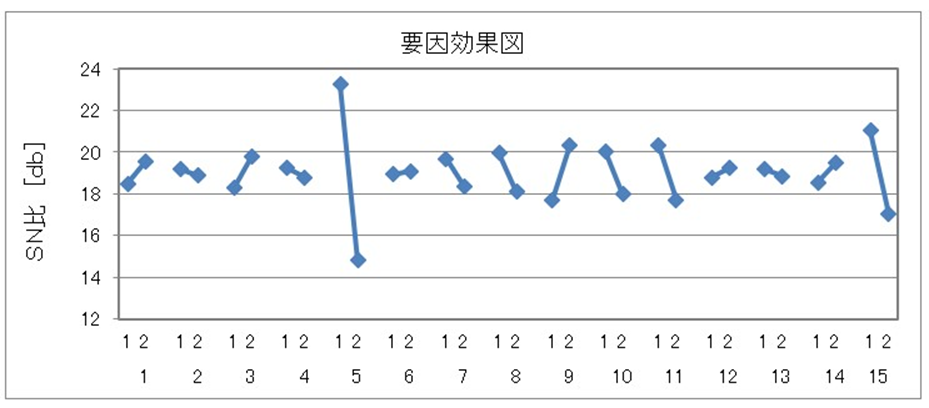
項目5がきいているのは明確にでていますが、それ以外に影響がありそうな項目がいくつかあるので、この要因効果図を参考に調査していくと何かわかるかもしれません。
まとめ
干し柿の乾燥条件の評価をMT法の各手法で行ってみました。データ数が少ないため不備もありましたが、各手法の特徴がなんとなく伝わったのではないかと思います。MTシステムでどんなことができるのか、どんなふうに使うのか、どの計算法が良さそうか、を考えるうえでの参考になれば幸いです。
追記
今回の解析の元になったのは、家の人が段ボール紙にマジックで記録したデータだけです。生産者の方が見れば分かると思いますが、今回のデータではきれいな干し柿をつくる条件は得られないでしょう。それは、重要な項目が抜けているからです。例えば重量変化,表面水分量,温度湿度の推移など。どんな情報が必要かを考え、そのデータを集めることが大切です。ただ、段ボールに書かれてた情報だけでも、ここまでの解析ができるのです。得られるものもありました。何事も実践しなければ判らないものです。手元にデータがあれば、まずはそれを使って解析してみるというのも良いと思います。